Note: 本文最初于 2011年02月06日 星期日 19:36 在 hi.baidu.com/lydrainbowcat 发表。
算法思想概述
本题是一道最大权闭合子图模型,应用的算法为最大流(BFS增广即可),定理为最大流最小割定理,辅助算法为拓扑排序。
问题初始建模
首先我们我建立图论模型,把每个植物当做一个顶点,植物携带的资源数目为顶点的权值。如果一个植物b在另一个植物a的攻击范围内,连接一条有向边<a,b>,表示a可以保护b。由于僵尸从右向左进攻,可以认为每个植物都被它右边相邻的植物保护,对于每个植物a(除最左边一列),向其左边的相邻植物b,连接一条有向边<a,b>。
由本题样例就可以发现,有一些植物是相互依赖的,于是我们可以进行算法实现的第一步:
1.使用拓扑排序去除图中的环,从而使图得到简化。
最大权闭合子图
进行算法的第二步。
2.对第一步中得到的图进行转置操作(把所有边反向),从而得到最大子权闭合图。
样例的图经过拓扑排序和转置操作后如下:
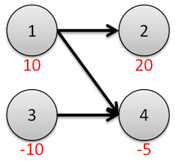
其中最大权闭合子图为(1,2,4)
下面进行算法实现的第3、4步:
3.最大权闭合子图的网络流建模:
(1). 建立附加源S和附加汇T。
(2). 图中原有的转置后的边容量设为∞。
(3). 从S向每个权值为正的点连接一条容量为该点权值的有向边。
(4). 从每个权值不为正的点向T连接一条容量为该点权值绝对值的有向边。
建模后图如下:
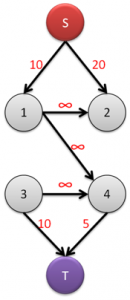
4.求解:求S到T的最大流Maxflow,最大权闭合子图的权值就是(所有正权点权值之和 – Maxflow),也就是需要输出的答案。
算法证明及复杂度分析
对于最大流最小割的详解,参见黑书《算法艺术与信息学竞赛》网络流部分第二道例题航天计划。
对于最大权闭合子图建图方法正确性的证明,参见胡伯涛《最小割模型在信息学竞赛中的应用》。
另有更为简便的、使用二元关系与最小割方程模型来证明的方法,博主在讲课的课件中曾多次提及,也可参见彭天翼《浅析一类最小割问题》。
参考程序
var a,f:array[0..601,0..601]of longint; d,score,link,incf,q:array[0..1000]of longint; yes,vis:array[0..601]of boolean; n,m,s,t,i,j,u,v,k,x,y,tot:longint; procedure topsort;//因为数据不大,写了个朴素的拓扑排序,没用栈和队列 var com:boolean; i,j:longint; begin com:=false; while not com do begin com:=true; for i:=1 to n*m do if d[i]=0 then begin dec(d[i]); yes[i]:=true; for j:=1 to a[i,0] do dec(d[a[i,j]]); com:=false; end; end; end; function maxflow:longint; function min(x,y:longint):longint; begin if x<y then exit(x) else exit(y); end; function bfs:boolean; var l,r,i,u,v:longint; begin fillchar(q,sizeof(q),0); fillchar(vis,sizeof(vis),0); l:=1; r:=1; q[1]:=s; vis[s]:=true; link[s]:=s; incf[s]:=maxlongint; while l<=r do begin u:=q[l]; for i:=1 to n*m+1 do if not vis[i] and(f[u,i]>0) then begin vis[i]:=true; inc(r); q[r]:=i; link[i]:=u; incf[i]:=min(incf[u],f[u,i]); if i=t then exit(true); end; inc(l); end; exit(false); end; procedure update; var u,v:longint; begin u:=t; while u<>s do begin v:=u; u:=link[v]; dec(f[u,v],incf[t]); inc(f[v,u],incf[t]); end; inc(maxflow,incf[t]); end; begin maxflow:=0; while bfs do update; end; begin readln(n,m); s:=0; t:=n*m+1; for i:=1 to n do for j:=1 to m do begin u:=(i-1)*m+j; read(score[u]); read(a[u,0]); for k:=1 to a[u,0] do begin read(x,y); v:=x*m+y+1; a[u,k]:=v; inc(d[v]); end; end; for i:=1 to n do for j:=1 to m-1 do begin u:=(i-1)*m+j+1; v:=(i-1)*m+j; inc(a[u,0]); a[u,a[u,0]]:=v; inc(d[v]); end; topsort; for i:=1 to n*m do if yes[i] then begin if score[i]>=0 then begin inc(tot,score[i]); f[s,i]:=score[i] end else f[i,t]:=abs(score[i]); for j:=1 to a[i,0] do if yes[a[i,j]] then f[a[i,j],i]:=maxlongint; end; writeln(tot-maxflow); end.


版本设置:1. 本服为微变版本,经验3000倍,最高等级255级,宝宝255级,开放1次转生,转生后200级玩家需要重新3转、4转职(避免重复转职,玩家可洗髓后再3转、4转职业),赠送1000点ap/次,游戏转职任务可无限转,所以手痒的玩家不要乱点哦,金钱设置100倍,锻造+12,金钱上限9.9E,适合长期入驻。2. 本服亮点:首创内功心法系统、好友跟随、好友定位、PK奖罚系统、BOSS刷新公告系统、套装系统、品质显示、银币商城、积点商城、声望商城、赌博系统、超炫锻造翅膀系统、女战士带刀、新地图【潜龙窟】、boss地图【若来谷】【魔界】【逐鹿战场】、文官任务每天做得大量点数、天书系统、单人副本
特色介绍:本服开放必杀合成 机械核心1个+机械原石10个+晶体原石5个+神石500 变废为宝开放王者首饰 需要王者图纸一个+晶体原石5个+王者原石5个+神石500开放技能守护无我,需要合成,详情见物品制作NPC1.主城设置罗尼特 开放 机械、锆石、必杀、守护。2.封杀加血辅助,影响游戏平衡的各类辅助。自带HOME助手3.添加 Ctrl + D 一键出售前两排物品、只清理0改装备武器4.游戏等级130级封顶。法师抗魔不转魔攻。5.物理职业3速满 ,法师释放88满,可以小抽.开放100级大罩。7.人物上线默认送24小时幸运和24小时兴奋 15000战斗经验 10000金币。下线后不扣时间8.开放